|
Sketching the History of Statistical Mechanics and Thermodynamics
(From about 1575 to 1980) |
© 1996-2024 HyperJeff Network
History | Philo | Physics | Blog [ Sources, Links, Notes ] |
| Anti- quity |
Ideas of atomism, that heat is a mode of motion within bodies and that pressure is the result of such motion, are all floating around. | |
|---|---|---|
| 1st cent AD | Hero of Alexandria (see also here) writes Pneumatics, an investigation on atmospheric air, summarizing a great deal of what was known at the time on syphons, pumps, the effects of heat on liquids, and engine designs. |
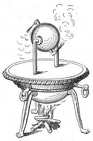 The aeolipile of Hero |
| 9th cent |
Al-Baqilani (d 1013) said to have introduced atomism to the Muslim Kalam (perhaps influencing Leibniz). | |
| 11th cent |
The loss of permanent magnetism when materials are subjected to high temperatures known in China. | |
| 13th cent |
Levi ben Abraham (1246-1315) includes a short passage noting that heat is a form of motion (for both light and matter) in his work, Liwyat Hen. | |
| 1575 | F Commandine translates Hero of Alexandria's Pneumatics into Latin (translated earlier in 1547 into Italian by Aleotti). | |
| 1612 | Santorre Santorio (see here also) (1561-1636) is known to have been using an early thermoscope and also writes Commentariar in artem medicinalem Galeni. Santorre writes to Galileo Galilei (1564-1642) including sketches of his device, to which Galileo replies that it was an invention of his. The priority remains unclear. | |
| 1615 | Thermoscopes of Santorio are sensitive enough to detect near-by body heat and candles. | |
| 1620 | Johannes van Helmont defines "gas" (the Flemish word for chaos) for air-like substances. | |
| 1638 | Galileo points out that simple pumps can only raise water about 32 feet, though this had been common knowledge to pump makers of the time. | |
| 1641 | Ferdinand II, Grand Duke of Tuscany, invents a thermometer using liquid in a glass tube with one end sealed, a slight improvement to Galileo's thermoscope. | |
| 1643 | Evangelista Torricelli (1608-1647) invents the barometer, also producing the first partial vacuum. | |
| 1644 | René Descartes' (1596-1650) treatise Principa Philosophiae published in Amsterdam. The work extends effords to formulate a fully mathematico-mechanical model of the world, including concepts of nonlocality, the absence of any vacuum and his vortex model of atoms. | |
| 1647 | Gilles Personne de Roberval (1602-1675) performed an oft-quoted experiment on air pressure whereby a carp's swim-bladder is partially removed, squeezed of almost all air and tied shut. The carp is then placed in a Torricellian vacuum and the bladder is observed to expand. | |
| 1648 | Florin Perrier experimentally shows that the height achieved by mercury in a barometer decreased as one scaled a mountain, a theoretical prediction of his brother-in-law, Blaise Pascal, and also known as the Puy de Dôme experiment. | |
| ca 1650 |
(Coffee begins to be important to and catch on in Europe.) | |
| 1651 | Jean Pecquet's (1622-1674) book on psychology popularizes the Roberval experiment (English translation in 1653). He also introduces the term "elater" as the tendency of air to expand, and theorizes that air on the earth's surface is compressed by the weight of the atmospheric air. | |
| 1654 |
Otto von Guericke's (1602-86)
experiment with two iron hemispheres held together by a strong partial vacuum being strong enough to resist the pull
of a train of horses on either side.
Ferdinand II invents the sealed thermometer. |
|
| 1660 |
Robert Boyle (1627-91)
publishes New Experiments Physio-Mechanicall, touching the Spring of the Air, and its Effects.
One experiment clearly shows the dependency on Torricelli's vacuum on ambient air pressure. Also presented
are discussions of both Pecquet's idea of air modelled by coiled-up wool-like or
spring-like atoms (which was preferred by Boyle) and of
Descartes'
idea of whirling particles which repell one another at short distances.
In response to Boyle's ideas, Franciscus Linus (1595-1675) proposes a theory whereby a vacuum is explained by the creation of an invisible collection of thread-like "funiculus," which strive to hold nearby objects together. Richard Townley (1628-1707) and Henry Power's (1623-1668) experiments establishing the PV law for expansion (the so-called "Boyle's Law" or "Marriotte's Law"). |
 Robert Boyle |
| 1661 | Boyle adds an appendix to his 1660 work, responding to the criticisms of Linus and Thomas Hobbes, presenting improved experimental results and giving a version of what is now known as "Boyle's Law" for the case of compression. | |
| 1662 | Boyle's "Defense of the Doctrine touching the Spring and Weight of the Air." | |
| 1663 |
Blaise Pascal (1623-1662)
writes On the Equilibrium of Liquids (published posthumously) suggesting that pressure is transmitted
equally in all directions in a fluid (later known as "Pascal's law"), probably discovered around 1648.
Power's book Experimental Philosophy, publishing early results on the PV law. |
|
| 1664 | Robert Hooke (1635-1703), using crude thermometers, establishes the constancy of the freezing point. | |
| 1669 | Johann Joachim Becher's (1635-1682) Subterranean Physics, a tract on alchemy and experimental results on minerals, introduces the idea that a "terra pingus" (oily earth) causes fire. (This idea is later picked up to form the phlogiston theory of heat.) | |
| 1670 | Boyle discovers that when acid interacts with certain metals a flammable gas is produced, known now as Hydrogen. | |
| 1673 | Christiaan Huygens (1629-95) builds a motor driven by the explosion of gunpowder. | |
| 1674 | John Mayow (1641-1679) suggests that air may consist of two different gases from experiments done on mice and candles, reported in his Five Medico-Physical Treatises. | |
| 1676 | Edmé Mariotte (~1620-1684) independently finds relationship between pressure and volume, in his work On the Nature of Air. (Known as "Mariotte's law" in France, and "Boyle's law" elsewhere.) | |
| 1684 | Hooke establishes the constancy of the boiling point. | |
| 1685 | Mariotte's The Motion of Water and Other Fluids published (posthumously). | |
| 1690 | Denis Papin (1647-1712) uses steam pressure to move a piston for the first time. | |
| 1697 | Georg Ernts Stahl introduces the idea of phlogiston as the agent of burning and rusting. | |
| 1698 | Thomas Savery invents the first modern heat engine | |
| 1701 | Isaac Newton (1642-1727) publishes "Scala graduum caloris et frigoris" in an attempt to improve on thermometer scales. | |
| 1702 |
Guillaume Amontons extrapolates the idea of absolute zero from the observation that
equal drops in temperature produce equal drops in pressure, and since pressure cannot become negative, there
must be a lower limit to temperature.
Ole Christensen Rømer devises a temperature scale based on the two phenomena of the boiling point of water and the temperature at which snow begins to form. |
|
| 1705 | Francis Hauksbee shows that sound needs air for propagation. | |
| 1712 | Thomas Newcomen's steam engine. | |
| 1714 | Daniel Gabriel Fahrenheit's (1686-1736) mercury thermometer introducing his temperature scale. | |
| 1716 | Jakob Hermann (1678-1733) proposes the first definite measure of the heat of molecular motion in his work on rational mechanics, Phoronomia. He postulates that (in modern lingo) pressure is proportional to density and to the square of the average velocity of the particles of motion. |
 Jakob Hermann |
| 1723 | Stahl's Foundations of Dogmatic and Experimental Chemistry popularizes phlogiston and the ideas of Johann Becher. | |
| 1724 | Hermann Boerhaave proposes that heat is a fluid of some sort. | |
| 1729 | Leonhard Euler (1707-1783), extending Johann Bernoulli's work on Descartes' vortex cosmology, models air with tightly-spaced, spinning spheres. He formulate an equation of state relating humidity, pressure, density and velocity, finding the Townley-Power-Boyle law as an approximation. He calculates air molecules to be about 477 m/s at mean conditions, and that this is about the speed of sound. | |
| 1730 | Johann Juncker's Conspectus of Chemistry systematically expands phlogiston theory. | |
| 1733 | Daniel Bernoulli (1700-1782), in a treatise on hydrodynamics worked out in the period from 1728 to 1733, gives a derivation of the gas laws from a billiard ball model, derives the Boyle-Mariotte relation and used conservation of mechanical energy to show that as temperature changes the pressure will change proportionally to the square of the particle velocities. This text marks the first truly statistical treatment of kinetic theory. A significantly updated edition of the text is published in 1738. The paper is all but forgotten until 1859. |
 Daniel Bernoulli |
| 1739 | George Martine establishes that the volume of an object is not proportional to the amount of heat it has. | |
| 1742 | Anders Celsius (1701-1744) publishes "Observations on two persistent degrees on a thermometer," basing his scale on the freezing point (100 degrees) and boiling points (0 degrees) of water. (The system is reoriented in 1745 by Carl Linnaeus, a.k.a. Carl von Linné.) | |
| 1744 | Mikhail Vasilievich Lomonossov publishes a paper on the causes of heat and cold, stating that heat is a form of motion. | |
| 1744 | (also, Carl von Linné, 1707-1778) reorients Celsius's scale. | |
| 1748 | Lomonosov formulates laws of conservation of energy and mass. Through about 1760, he performs a number of theoretical investigations about molecular structures, speculating on the effects of translation, vibration, and rotations of such molecules. | |
| 1756 | William Cullen's An Essay on the Cold Produced by Evaporating Fluids and some Other Means of Producing Cold. | |
| 1758 | Rudjer Giuseppe Boskovic (1711-1787) publishes Theoria Philosophiae Naturalis, the first attempt to use Newton's laws to account for all physical phenomena as the interaction of point particle acting at a distance. Molecules are modeled as subjected to intermolecular forces which are attractive nearby but repulsive at greater distances. His efforts, however, are too vaguely worked out to base a theory on. | |
| 1760 |
Joseph Black (1728-1799)
invents the calorimeter.
Ebenezer Kinnersley (1711-1778) performs an experiment devised by Benjamin Franklin (1706-1790) to establish the connection between heat and electricity, leading to an electric thermometer. |
|
| 1761 | Black introduces the notion of latent heat, finding that when melting ice, heat can be absorbed without changing temperature. (Black never publishes his results, however.) | |
| 1765 | James Watt invents his steam engine, using two separate (hot/cold) cylinders, and is over six times more effective than Newcomen's. | |
| 1772 | Johan Carl Wilcke (1732-1796) calculates the latent heat of ice (independently of the work of Black). |
Phlogiston Theory (~1660's to ~1790's) Kinetic Heat Theory (~1716 to ~1760's) (then ~1816 to present) Caloric Heat Theory (~1780's to ~1860's) Wave Theory of Heat (~1830's to ~1860's)
Statistical Mechanics |
| 1781 | Wilcke comes up with the concept of specific heats. | |
| 1782 | Antoine Lavoisier (1743-1794) establishes an early version of the conservation of matter through his finding of constancy of weight before and after chemical reactions. | |
| 1783 | Lavoisier's work, Reflections on Phlogiston, on the weaknesses of phlogiston theory with respect to combustion. | |
| 1786 |
Lavoisier and
Laplace's work
Memoir on Heat.
Benjamin Thompson (Count Rumford) (1753-1814) publishes his New Experiments on Heat, among other things introducing the notion of convection, distinct from heat conduction. |
|
| 1787 | Jackues-Alexandre Charles determines that at a given temperature change, different gases expand the same amount (known as "Charles's law"). | |
| 1789 | Lavoisier's book Elementary Treatise on Chemistry, containing the law of mass conservation. | |
| 1791 |
Richard Kirwan (~1733-1812), previously a staunch defender of phlogiston theory,
concedes that the experimental evidence says otherwise.
Pierre Prévost's theory of heat and radiation exchange, stating that cold is the absence of heat, hot bodies radiate continually and that a lack of radiation indicates equilibrium with surroundings temperature. Jeremias Richter (1762-1807) founds stoichiometry, the principle of fixed chemical reactions. |
|
| 1798 | Cannon-boring experiments of Rumford demonstrating the conversion of work into heat in his work Enquiry Concerning the Source of Heat which is Excited by Friction, showing also that additional weight of an object due to heating (a prediction of caloric theory) was not detected. | |
| 1799 |
Ice-rubbing experiments of Humphrey Davy (1778-1829) demonstrating the conversion of
work into heat, and suggesting that an indefinite amount of heat could be generated from a body (whereas caloric
theory severely limits its available amount).
Joseph-Louis Proust formulates that elements in a compound always combine in definite mass ratios ("Proust's Law"). |
|
| 1800 | William Herschel (1792-1871) publishes "An investigation of the powers of prismatic colours to heat and illuminate objects" investigating the effects of different wavelengths of light on a thermometer, finding light just beyond the red to be the hottest. | |
| 1801 |
Johann Ritter discovers ultraviolet radiation while doing
work with silver chloride.
John Dalton (1766-1844) finds that two gases in the same region produce the same pressure as if they occupied the region alone, known as the law of partial pressures. |
|
| 1802 | Joseph-Louis Gay-Lussac (1778-1850) finds that, at a given pressure, the change in volume is proportional to the change in temperature. | |
| 1803 |
Dalton formulates his atomic theory of matter, stating that
chemicals are formed by integer numbers of atoms, by studying the weights of chemicals and reactants.
Claude-Louis Berthollet demonstrates that reaction rates depend on both the amount of substances present as well as their affinities in his work Essay on Static Chemistry. William Henry finds that a gas's mass when dissolved in a liquid is proportional to the pressure (later known as "Henry's law"). |
|
| 1804 | John Leslie (1766-1832) writes An Experimental Inquiry into the Nature and Propagation of Heat, showing that light and radiated heat have similar properties. | |
| 1805 |
Pierre-Simon Laplace (1749-1827)
formulates his theory of capillary forces based on his studies of molecular forces in liquids.
William Wollaston (1766-1828) suggests using mechanical work as a means of measuring the amount of heat in a combustion engine. |
 Pierre-Simon Laplace |
| 1806 |
Thomas Young (1773-1829) formulates a precursor to the
modern formulation of energy, mathematically associating it with mv2 (twice the modern "kinetic energy").
Young's System of Chemistry contains the first published account of Dalton's ideas on atomic theory. |
|
| 1807 | Jean Baptiste Joseph Fourier (1768-1830) completes his On the Propagation of Heat in Solid Bodies, introducing many mathematical novelties, including his series expansion techniques. |
 Jean Fourier |
| 1808 | (Dec 31st) Gay-Lussac states that gases chemically combine in exact proportions of volume. | |
| 1811 |
Siméon-Denis Poisson
(1781-1840) develops his mathematical theory of heat, based on the work of
Fourier.
Amedev Avogadro (1776-1856) hypothesizes that the "number of integral molecules in any gases is [...] always proportional to the volumes", and that the ratio of the masses of molecules is proportional to the ratio of gas densities at equal temperature and pressure (later becoming "Avogadro's law"). Jöns Jakob Berzelius states that electrical and chemical forces are one and the same and that atoms are electrically charged, in his work Theory of Chemical Proportions and the Chemical Action of Electricity. |
|
| 1812 |
Davy writes Elements of Chemical Philosophy, including a hypothesis that
in addition to the vibrational and undulatory motion of solids, gasses as well exhibit rotational motion about an axis.
Delaroche and Bérard's measurements of specific heats at atmospheric pressure of a large number of gasses. Their measurements agreed with Laplace's predictions and remained a cornerstone for caloric theory. |
|
| 1816 | John Herapath (1790-1868) writes, "On the physical properties of gases," essentially proposing the same theory, but developed independently, as that of Daniel Bernoulli. | |
| 1819 | Pierre-Louis Dulong and Aléxis Thérèse Petit (1791-1820) find constant specific heat at constant pressure for metals over wide range of temperatures, finding that the product of the specific heat and the atomic mass remains constant (known as the "Law of Dulong and Petit"). | |
| 1821 |
Herapath publishes, "A mathematical investigation into the causes, laws, and
principal phaenomena of heat, gases, gravitation, etc," in the Annals of Philos.
He explained in outline how kinetic theory could give accounts of sound propagation, phase changes and diffusion.
The paper is all but ignored due to rejection by the Royal Society of London, and Humphry Davy in particular.
Thomas Johann Seebeck discovers a process by which heat is converted into electricity in the junction of some metals, known as theormoelectricity. |
|
| 1822 |
Fourier's
essay Analytic Theory of Heat is published, furthering his techniques of analysis.
Charles Cagniard de la Tour, in liquification experiments, finds that both temperature and pressure must be appropriately controlled, and discovers what is now know as the critical point of a substance. |
|
| 1824 |
Sadi Carnot
(1796-1832) publishes "Reflections on the Motive Power of Fire," introducing the ideal gas cycle analysis,
showing that when heat passes between two bodies theormodynamic work (which he defines) is done,
and proposes an idea for an internal combustion engine.
Pierre-Simon Laplace (1749-1827) publishes several papers refining an idea of Newton's that gasses are formed through repulsive interactions. |
 Sadi Carnot |
| 1827 | Robert Brown (1773-1858), investigating the well-known irregular motions seen of particles suspended in liquid under a microscope, shows that such motions cannot be attributed to any vitality of the particles themselves, through studies of many organic and inorganic substances. | |
| 1829 |
Gustave-Gaspard Coriolis defines the term "kinetic energy" in his studies published
as On the Calculation of Mechanical Action.
Thomas Graham (1805-1869) experimentally uncovers the law of gas diffusion, by which the rate of a gas's diffusion, squared, is proportional to its density. |
|
| 1833 | Heinrich Friedrich Emil Lenz determines that resistence in metals increases with temperature. |
 William Thomson |
| 1834 |
Clapeyron formulates the first version of the second law of thermodynimcs, based on
studies of steam engines.
Jean-Charles-Athanase Peltier shows that heat can be absorbed or given off when current is passed one way or the other across a junction between two different metals (knows as the Peltier effect). James David Forbes (1809-1868) establishes the correlation of thermal and electrical conductivities for solids. |
|
| 1837 |
von Suerman's experiments on air at reduced pressures verifying
Clappeyron's version of Carnot's formulas.
Herapath publishes an article deriving the speed of a molecule in a gas (derived 4 years earlier). |
The 1840's were marked by the nearly simultaneous and independent conceptualization of the conservation of energy by Mayer, Joule, Helmholtz and Ludvig August Colding (1815-88). |
| 1842 |
Julius Robert Mayer (1814-1878) clearly formulates the conservation of energy,
and that heat is a form of (mechanical) energy.
William Thomson, Lord Kelvin's (1824-1907) On the Uniform Motion of Heat in Homogeneous Solid Bodies. |
|
| 1843 |
(through 1848) Through a series of experiments,
James Prescott Joule
(1818-1889) establishes the exact relationship between heat and mechanical work.
(Joule's work is little read.)
John James Waterston (1811-1883) anonymously publishes Thoughts on the Mental Functions containing in a note at the end a full and accurate account of the kinetic theory of gases and the introduction of the idea of a mean free path. The work goes all but completely unread. |
|
| 1845 | Waterston submits a papers on the kinetic theory of gases to the Royal Society, who rejects it. The paper precisely lays out the ideas of energy equipartition and gives the first modern kinetic definition of temperature. A short abstract appears a year later, and again in 1851, but the work is ignored. | |
| 1847 |
Herapath's Mathematical Physics published,
deriving properties of gases from the vis viva of molecules.
Joule publishes "On Matter, Living Force, and Heat" in the Manchester Courier, stating the principle of the conservation of energy and giving the conversion from heat to kinetic energy. Rudolf Clausius (1822-88), spurred on by Krönig's paper "The Foundation of the Theory of Gases," publishes "The Nature of the Motion Which We Call Heat" on the relation of vis viva to heat. Hermann Ludwig Ferdinand von Helmholtz (1821-94) publishes his On the Conservation of Energy, extending Carnot's princple of the 'impossibility of unlimited moving force' (kinetic energy) to a mathematical formulation of the 'principle of conservation of living force' (vis viva / kinetic energy). (Independent of Joule's publications.) John William Draper finds that all substances begin to glow around 525°C, starting in the red and eventually becoming white. |
 James Joule |
| 1848 |
Joule
reads a paper using Herapath's kinetic theory. The paper contains the first
numerical results from the kinetic theory. (Not published until 1851, and not well known until
Clausius's
reference to it in 1857.)
William John Macquorn Rankine's (1820-1872) researches into mechanics and heat (mainly through 1855). Kelvin develop's a scale of absolute temperature (now known as the "Kelvin" scale) based on the theory of Carnot. |
|
| 1849 |
James Thomson (1822-1892), using Carnot's theories, predicts the
lower of the freezing point of water under high pressures.
Kelvin, in speaking of Carnot's theory, coins the term "thermodynamics." |
|
| 1850 |
John Herschel (1792-1871)
publishes (anonymously, though generally known) an article on Quetelet's work in statistics,
introducing much of the continental work on statistics to British scientists.
Clausius gives a verbal formulation of the second law, for which there is no mechanism whose only function is the transfer of heat. |
 Hermann von Helmholtz |
| 1851 | Kelvin independently rediscovers the idea of absolute zero (149 years after Amontons), extrapolating from Charles' law that it must be about -273°C, and suggesting that the energy of the molecules would tend to zero. He also derives the second law of thermodynamics using Carnot's ideas. | |
| 1852 |
Henri-Victor Regnault (1810-1878) shows that gas behavior doesn't quite follow Boyle's law at low
temperatures and extrapolates a value of -273°C for absolute zero.
Joule and Kelvin show that expanding gases become cooler in the process, the latter giving the first general statement of the principle of the "universal tendency toward dissipation of energy." |
|
| 1854 |
Hendrik Roozeboom experimentally determines the phase law, later derived mathematically by
Gibbs.
Clausius coins the term "entropy" from the Greek word for transformation, τροπη. He proposes the amount of energy in the universe is constant and that the entropy of the universe is constantly increasing. He uses the function dQ/T as a way to compare heat flows with heat conversions, stating the 2nd law as the closed integral over a reversible cycle of dQ/T >= 0. |
 Rudolf Clausius |
| 1855 | Rankine's Outlines of the Science of Energetics. | |
| 1856 | Karl Krönig (1822-79) writes a paper suggesting that gas molecules in equilibrium travel in straight lines until they collide with something, published in Poggendorfs Annalen der Physik. Whereas the efforts of Bernoulli, Euler, Herapath, Hermann and Joule were largely ignored, Karl Krönig's efforts were widely read, though not constituting an advance in kinetic theory. | |
| 1857 | Clausius publishes a paper on a mathematical kinetic theory, explaining evaporation and establishing heat as energy distributed statistically among particles. | |
| 1858 | Clausius introduces the idea of the mean free path of a particle in working out a kinetic theory of diffusion. | |
| 1859 |
James Clerk Maxwell
(1831-79) reads a paper on kinetic theory, printed in 1860 as "Illustrations of the Dynamical Theory of Gases,"
using random velocity distributions for gases, and showing viscosity to be independent of temperature. The
paper is originally intended to show internal inconsistencies in the kinetic theory, but through its rigor
it greatly refined the theory and provided new insights.
Gustav Robert Kirchhoff (1824-1887) derives from the second law of thermodynamics that objects cannot be distinguished by their thermal radiation at a given uniform temperature, one must also use reflected light. Bernoulli's paper republished due to renewed interest in kinetic theory. (Herapath henceforth goes into obscurity.) |
 James Clerk Maxwell |
| 1860 |
Michael Faraday's paper "Pressure Melting Effect" describing the lowering of the freezing
point of water using pressure.
Maxwell shows a discrepancy between the prediction by kinetic theory of the specific heat of diatomic gases and experiment. (Not to be resolved satisfactorally until the early stages of quantum theory.) This paper is the first of four works on kinetic theory by Maxwell, bringing a new level of rigour and sophistication to the theory. |
|
| 1861 |
Thomas Andrews (1813-1885), in a series of experiments with CO 2
through 1869, finds that at low temperatures Boyle's law breaks down, and there are regions on a PV chart where,
for a given isotherm, changes in volume produce no change in pressure. This region is recognized to be the
liquid-vapour equilibrial state. He rigorously finds the critical point and triple point.
Kirchhoff formulates the notion of a blackbody. Heinrich Gustav Magnus (1802-1870) experimentally determines the thermal conductivity of Hydrogen gas, showing that it conducts heat as metals do. |
|
| 1863 |
John Tyndall's (1820-1893) Heat as a mode of Motion, popularizing
Maxwell's ideas on heat.
Andrews shows that, contrary to expectations, above a substance's critical point it may be continuous changed from gas to liquid and vice versa through variations of temperature and pressure. |
|
| 1864 | Clausius publishes Mechanical Theory of Heat, the first treatise on thermodynamics. Vol 2 publish in '69, dealing with applications to electricity. A second edition, published as a textbook, was finished in '75. English translation in 1867 (Vol 1 only), and French in 1868 (both volumes). | |
| 1865 |
Clausius
uses Carnot's
techniques to derive "entropy" (and shows the two laws of thermodynamics expressible in the same ways as the older
caloric theory), a term coined for the quantity defined early by him, dQ/T. In a public speech entitled
"The entropy of the universe tends to a maximum," he shows how thermodynamics seem to imply an
eventual heat death for the universe.
Josef Loschmidt's (1821-95) points out that Maxwell's conclusion that the proportionality of the mean free path to V/Nd2 could be used to estimate the size of an atom. With further considerations, he estimates the size of an air molecule to be about 10-7 cm, about 4 times too large, but the best estimate to date. |
|
| 1866 | Maxwell models interatomic forces by a inverse fifth-power law, though only as an interim solution. | |
| 1867 |
Maxwell publishes
his major work on kinetic theory, On the Dynamical Theory of Gases.
Kelvin's On Vortex-Atoms. (Spurred on by Maxwell's work, serious debates on the statistical interpretation of irreversibility begin.) |
|
| 1868 | Ludwig Boltzmann's (1844-1906) extends Maxwell's distribution law to include external forces. In the case of gravity, he worked through the distribution of densities and pressures and that thermal equilibrium was maintained. |
 Ludwig Boltzmann |
| 1871 |
Maxwell, helping out
P G Tait, who was drafting an textbook on thermodynamics, comes up with his
parabol of the daemon to conceptually explain heat statistics.
Boltzmann suggests that one may derive the probabilistic picture from the kinetic one by heuristically assuming that all microstates must be realized in a system before returning to a specific microstate, and thus measured values should average the effects of such states. (Known as the "ergodic theorem," and so named by Ehrenfest in 1911.) James Thomson suggests that even below the critical point, a substance may smoothly transition between gas and liquid from considerations of experimental data on pressure and volume. |
|
| 1872 | In a 100-page paper entitled, "Further Studies of the Thermal Equilibrium of Gas Molecules," Boltzmann's derives his transport equation (Η-Theorem), showing explicitly that isolated systems must always evolve in such a way that entropy increases. He introduces a number of mathematical innovations, including a technique of discretizing the allowed energy levels for a molecule, and allowing this energy bin to go to zero. Little read at first, the paper later meets with wide-spread opposition. | |
| 1873 |
Josiah Willard Gibbs (1839-1903)
publishes Graphical Methods in the Thermodynimcs of Fluids
and A Method of Geometrical Representation of the Thermodynamic Properties of Substances by Means of Surfaces,
introducing many new graphical techniques.
From 1873 to 1878 he publishes a series of important articles in the
Transactions of the Connecticut Academy of Arts and Sciences,
widely influencing scientists in the US and in Europe.
Johannes Diderik van der Waals (1837-1923), in doctoral dissertation, gives the first correct approximation for the effects of a non-vanishing ratio of molecule diameter to average distance by assuming long-range attractive and short-range repulsive forces, applying this to the case of gases at high densities. Using his "equation of state," he gives the first successful attempt to explain a (gas-liquid) phase transition. The theory both accounted for Andrews's critical point phenomena and confirmed James Thomson's hypothesis. |
 Josiah Gibbs |
| 1874 | Kelvin points out that the irreversibility of Boltzmann's kinetic theory seems to contradict the underlying classical laws of physics remaining time-invariant (the so-called "reversibility paradox," sometimes attributed to Loschmidt). | |
| 1876 |
Gibbs
publishes the first part of On the Equilibrium of Heterogeneous Substances (the 2nd part in 1878).
The works deal with chemical reactions, phase equilibrium and the use of free energy.
(Karl Paul Gottfried von Linde builds the first practical refrigerator using liquid ammonia.) |
|
| 1877 |
Boltzmann
formulates a statistical mechanical version of the second law of thermodynamics in the paper,
"On the Relation Between the Second Law of the Mechanical Theory of Heat and the Probability Calculus
with Respect to the Theorems on Thermal Equilibrium". There he formulates that the entropy of a system is
proportional to the log of the phase space volume occupied by the macrostate of the system,
S = k ln Ω, making use of his mathematical innovation of using finite areas
of phase space.
Liquification of oxygen achieved, after nearly one hundred years of trying, by Louis Paul Cailletet (1832-1913) (on Dec 2nd) and Raoul Pierre Pictet (1846-1929) (on Dec 22nd). |
|
| 1878 | Maxwell's "On Boltzmann's Theorem on the Average Distribution of Energy in a System of Material Points" develops the full ensemble technique in analyzing statistical distributions. | |
| 1879 |
Josef Stephan
(1835-1893) determines that the amount of radiation given off by a body through heating
is proportional to the fourth power of its temperature (known as the "Stephan-Boltzmann law"),
Rτ = σT4.
Max Karl Ernst Ludwig Planck (1858-1947) publishes his doctoral thesis, "On the Second Law of Mechanical Theory of Heat," reformulating the 2nd law as S1 - S2 >= 0. |
|
| 1884 |
Boltzmann
(1844-1906) succeeds in theoretically deriving the radiation law found by Stephan,
showing that a mechanical pressure and energy density must be associated with the radiation
in order to satistfy the second law.
Gibbs coins the term "statistical mechanics" for the kinetic theory's treatment of thermodynamic issues. |
|
| 1885 |
Lodge promotes the idea that mechanical energy can be localized and flow,
as inspired by the work a year earlier by Poynting in electromagnetic theory.
Johann Jakob Balmer (1825-1898) finds a formula for describing the four spectral wavelengths then known for hydrogren as found by Ångstrom. |
|
| 1889 |
Jules Henri Poincaré
(1854-1912) derives his recurrence theorem, whereby a system with fixed total and volume will eventually
return arbitrarily closely to any given state.
Gibbs' last work, Elementary Principles in Statistical Mechanics. |
|
| 1890 | Edward Parnell Culverwell (1855-1931) points out the apparent contradiction between Boltzmann's H-theorem and the irreversibility of the micromechanical processes on which it is based, suggesting that some kind of irreversible process takes place at this micro level, perhaps in connection with the ether. | |
| 1893 | Wilhelm Carl Werner Otto Fritz Franz Wien (1864-1928) experimentally finds that the wavelength of maximum radiation of thermal body is proportional to the inverse of its temperature (known as "Wien's law") using an oven with a small hole as an approximation to a theoretical black-body. | |
| 1894 | S H Burbury points out that the H-theorem relies on the uncorrelated nature of molecular interactions, but that this may not be valid after an individual collision, and hence not in general valid without some external randomizing element. Boltzmann calls this the hypothesis of molecular disorder, specifically referring to the low probabilitiy of two molecules colliding twice within any significant time frame, but mentioning that this would become an issue for gases at high densities. | |
| 1895 |
Pierre Curie (1859-1906), in his doctoral dissertation, defined both ferro-, dia-,
and paramagnetism, showing that ferromagnets lose their magnetic properties as their temperature
is increased, eventually losing it completely above a certain temperature specific to that material (the "Curie point").
He suggests that diamagnetism is an atomic property, while the other two are properties of bulk matter.
Wilhelm Röntgen (1845-1923) discovers a new penetrating kind of radiation, dubbed X-rays. |
|
| 1896 |
Ernst Zermelo (1871-1953), starting with the postulate that the second law
is true, tries to show the inherent contradictions of the purely mechanical basis of statistical mechanics, making use of
Poincaré's
result on recurrence (his "recurrence paradox").
Wien proposes an explicit form for the black body distribution law, ρ = αν3exp{-βν/T}, which fits the existing data. Antoine Henri Becquerel (1852-1908) discovers radioactivity in fluorescent materials. |
|
| 1897 | Joseph John Thomson (1856-1940) demonstrates that cathode rays were electrically charged particle streams, know shortly thereafter as electrons. |
 Max Planck |
| 1898 | Boltzmann publishes his Lectures on Gas Theory. | |
| 1899 |
Otto Lummer (1860-1925) and
Ernst Pringsheim
complete the first accurate measurements of the spectral radiancy of blackbodies, showing the breakdown
of Wien's law at high temperatures and low frequencies.
Emile Hilaire Amagat publishes The Laws of Gases of extensive experiments with gases under very high pressures. JJ Thomson and Philipp Lenard (1862-1947) begin experimental investigations of photoelectric radiation. Planck finishes part 5 of his work, begun in 1894, on the foundations of electromagnetic irreversible processes in black bodies, ultimately based on techniques pioneered by Boltzmann. |
|
| 1900 |
Kelvin
proposes a modification to Wein's law of the form
ρ ~ ν2exp{-βν/T}.
Planck, studying blackbody radiation and following Boltzmann's techniques of dividing the energy continuum into cells, proposes fixing cell sizes to be proportional to oscillator frequency, and in so doing derives the correct radiation spectrum for blackbodies. Planck proposes the constant, h (Planck's constant), as a quantum of action in phase space. |
Planck's 1900 analysis did not, at the time, imply any new law about the microstructure of matter, nor was there any reason to believe that extrapolation of the Rayleigh-Jeans law signalled any failure of classical methods. |
| 1902 | Gibbs publishes Elementary Principles in Statistical Mechanics, his treatise on the subject, deriving common thermodynamic properties from particle statistics, giving his full account of ensemble theory and their relationships (including the so-called "Gibbs paradox," though there was nothing paradoxical about it at the time). This work, and independently in an article in the same year by Albert Einstein (1879-1955), presents the first explicit generalization of gaseous and thermal theory to statistical mechanics. | |
| 1903 | Einstein paper, "A Theory of the Basis of Thermodynamics," presents a greatly generalized measure of state probability and the relationship with entropy and temperature. | |
| 1905 |
Marian Smoluchowski (1872-1917) and
Einstein
independently investigate Brownian motion, the motion of very small particles suspended in liquid.
This is shown to be an observable effect of the fluctuations of statistical mechanical movement,
despite producing no net effect on average.
Einstein publishes a paper on the photoelectric effect, basing his analysis on an analog of the statistical mechanical approach for classical electromagnetic fields modelled as quanta of light. Few physicists accept the idea before the discovery of the Compton Effect in 1922. Paul Langevin (1872-1946) developes a more satisfactory theory of para- and diamagnetism, applying statistical mechanics to gases of molecules with permanent dipole moments, also explaining the inverse temperature dependence of paramagnetic susceptibility, though later shown by Bohr to be inconsistent with statistical mechanics obeying classical mechanics. |
|
| 1906 |
Walther Nernst (1864-1941) formulates his "heat theorem," stating that in the limit of absolute
zero temperature, both the entropy change and the heat capacity go to zero (subsequently recognized as the Third
law of thermodynamics).
Pierre Weiss (1865-1940) creates general theory of paramagnetic to ferromagnetic transitions. |
 Albert Einstein |
| 1907 |
Andrei Andreyevich Markov
(1856-1922) develops his theory of linked probabilities.
Einstein publishes a paper on the specific heats of solids, deriving the law of Dulong-Petit from atomic oscillators confined to quantized energies, working out well with the recent theorem of Nernst. Pierre Weiss explains ferromagnetism by way of small domains of magnetic polarization within a material. |
|
| 1908 |
Jean-Baptiste Perrin calculates the approximate size of a water molecule
in experimental tests of Einstein's
work on Brownian motion, further convincing many of the atomic hypothesis.
Planck begins formulating derivations of the black-body law starting with an assumption of energy quantization. JJ Thomson solidifies his "plum-pudding" model of the atom. |
|
| 1909 |
Constantin Carathéodory
publishes a purely mathematical and axiomatic account of thermodynamics.
Einstein corrects the blackbody derivation of Planck, which was technically only valid for hν<<kT. |
|
| 1910 | Jean Perrin experimentally shows that the theoretical predictions of Einstein's calculations on Brownian motion are in agreement, becoming for many the best extant proof of the existence of atoms. | |
| 1911 |
Ernst Rutherford (1871-1937) proposes the nuclear model of the atom.
Planck's first paper explicitly quantizing the allowed radiation of oscillators in a blackbody. Arnold Sommerfeld (1868-1951) notes that elementary regions of phase space should be related to Planck's constant. Otto Sackur (1880-1914) suggests the need for an absolute definition of entropy, in order that quantum systems be taken into account (suggesting that phase space be divided into cells of volume h3). Ladislaw Natanson proposes that Planck's law is the result of the indistinguishability of states of light quanta. Niels Henrik David Bohr (1885-1962) defends his dissertation and begins constructing atomic models which try to forge a connection with Planck's constant as a fundamental constant of quantization. Heike Kamerlingh Onnes (1853-1926) experimentally finds that mercury will become superconductive when cooled very close to absolute zero and also discovers superfluidity. Paul (1880-1933) and Tatiana Afanassjewa Ehrenfest (1876-1964) publish a work giving a detailed criticism of the ensemble theories in statistical mechanics. Nernst's experiments with many substances, shows specific heats going to zero at absolute zero in general, providing strong support for the new quantum theories. |
|
| 1912 |
Poincaré
proves that one can invert the Planck distribution via a Fourier transform and deduce that
black-body radiation implies a quantization of energy states.
Sackur and H Tetrode independently solve Boltzmann's Law to obtain S = Nk ln[(2ρmkT)(3/2)V/Nh3] + (5/2)Nk
showing a need for quantization in classical gas laws.
|
|
| 1913 |
Artur Rosenthal (1887-1959) and Michel Plancherel (1885-1967)
prove that the ergodic hypothesis is not viable for any dynamical system (opening the way to
the quasi-ergodic hypothesis and certain theorems in ergodic theory).
Paul Ehrenfest shows how to estimate rotational effects of a diatomic gas on specific heat by replacing integrals with sums over discrete contributions from quantized states. The work is later refined by E Holm (1913) and by Planck (1915). Bohr's article, "On the Constitution of Atoms and Molecules." |
|
| 1916 |
Robert Andrews Millikan (1868-1953), in experiments with the photoelectric effect,
both confirms the theoretical work of
Einstein
and confirms the value of
Planck's
constant independent of work done with blackbodies.
Einstein produces a derivation of the black-body radiation distribution with the assumption of both spontaneous as well as stimulated emission of radiation by matter. Nernst predicts a state of degeneration can be reached for any gas at a low enough temperature, through extensions of his thermodynamic theory. Sydney Chapman (1888-1970) and David Enskog (1884-1947) develop ways to solve the Maxwell-Boltzmann tronsport equations for a general class of inter-molecular force laws. Gilbert Newton Lewis (1875-1946) devises a theory of molecular bonding based on atoms consisting of a series of concentric cubes, the edges of which may share electrons with other atoms. (The idea is popularized, starting in 1919, by Irving Langmuir (1881-1957).) |
|
| 1917 | Arthur Stanley Eddington (1882-1944) publishes a paper on radiative equilibrium, suggesting that the ionization of atoms in stars. | |
| 1920 |
Meghnad Saha (1893-1956) writes,
"Ionization in the solar chromosphere," analyzing spectral lines
of stars as atomic dissociation in the chromosphere, where lower pressures override the lower temperatures of a star,
also (in a second paper) predicting that lower-temperature sun-spots will show lines of rubidium and cesium
(an effect detected in 1922 by H N Russell).
Wilhelm Lenz (1888-1957) models crystals by a lattice of dipolar atoms which feel nearest-neighbor interactions, obtaining the Curie law for magnetization and suggestions its applications to ferromagnetism. |
|
| 1922 |
Louis Victor Pierre Raymond duc de Broglie
(1892-1987) applies Sackur's technique of quantizing
phase space to derive the Wien distribution law for energy density:
du = (8ρh/c3) exp(-hν/kT) ν3 dν
Charles Darwin (1887-1962) and Ralph Howard Fowler (1889-1944) publish "On the partition of energy," developing a new approach to evaluating statistical probabilities using complex analysis and the method of steepest descent. |
|
| 1923 | Lewis's Thermodynamics and the Free Energy of Chemical Substances, bringing thermodynamics in closer contact with chemistry. |
 Satyendranath Bose |
| 1924 |
(June) Satyendranath Bose (1894-1974)
sends Einstein
a copy of his paper, containing a new derivation of Planck's radiation law based purely on photon statistics,
after it was rejected by Philosophical Magazine.
Einstein
translates it into German and submits it to the Zeitschrift für Physik for him with a recommendation.
Einstein presents a paper showing that in the limit of high temperatures, a gas of indistinguishable Bose particles approaches the characteristics of a Boltzmann gas. de Broglie writes two papers in the Comptes rendus of the Paris Academy elaborating on a fundamental principle of wave-particle duality. The works mature into his 1925 doctoral thesis. |
|
| 1925 |
Max Born (1882-1970),
Werner Karl Heisenberg
(1901-1976), and Pascual Jordan formulate quantum mechanics based on the
mathematics of matrix algebra.
Einstein, citing works by Bose and de Broglie, suggests that the analogy between quantum gases and molecular gases are complete, and that both photons and molecules have both particle and wave characteristics. He also points out that molecules at low temperatures cannot be considered independent entities, even in the absence of intermolecular forces, and will form a quantum condensate. Samuel A Goudsmit's (1902-1979) hypothesis an extra degree of freedom to electrons termed "spin" due to the mathematical similarity to classical spin. Later, with George Eugene Uhlenbeck (1900-1988), half-integer quantum numbers are introduced in the theory of the hydrogen atom. Wolfgang Pauli (1900-1958) formulates the exclusion principle for the electron, accounting for a number of chemical properties in atoms and molecules. Planck devises a new derivation of thermodynamic formulas for Boltzmann gases using the formulations, z = exp(-ξ/kT), Z = zN / N!
Ernst Ising (1900-), following the investigations of Lenz, publishes a paper dealing with magnetic models via dipolar atomic interactions. |
|
| 1926 |
Born introduces into
quantum mechanics his probability interpretation of interactions.
Enrico Fermi (1901-1954) derives the statistical properties of gases which obey the Pauli exclusion principle. Erwin Rudolf Josef Alexander Schrödinger (1887-1961) developes a second formulation of quantum theory in terms of wave mechanics independently. Paul Adrien Maurice Dirac (1902-1984) relates the symmetry of quantum mechanical wave functions to the statistics of Bose, Einstein and Fermi. He also derives the Planck distribution from first principles. Eddington's The Internal Constitution of the Stars, relating the radiation pressure of stars to their luminosity. Fowler shows that some of the properties of white dwarf stars could be accounted for by treating them as (Fermi) quantum degenerate gases, being an early example of quantum statistics explaining the properties of large macroscopic objects. Robert Hutchings Goddard launches the first rocket, using liquid fuel and reaching a height of 184 feet and 60 miles per hour. |
 Paul Dirac |
| 1927 |
John von Neumann
(1903-1957) formulates a fully quantum mechanical generalization of statistical mechanics.
Bohr pronounces his notion of complimentarity in quantum theory. Heisenberg formulates the uncertainty principle of quantum mechanics. Dirac and Pauli independently propose to model metals with molecules obeying Fermi-Dirac statistics. Pauli explains the paramagnetic susceptibility of metals using electron spin and the exclusion principle. Willem Hendrik Keesom (1876-1956) and M Wolfke find discontinuities in several properties of helium at very low temperatures and suggest that it may be due to a phase change, calling them helium I and II. Walter Heitler (1904-) and Fritz London (1900-1954) apply Heisenberg's resonance theory to the covalent molecular bond between two hydrogen atoms, showing stability to a function of electron spins, and arguing against the stability of such helium bonds. |
|
| 1928 |
Sommerfeld
treats electrons in metals as a degenerate Fermi gas using the new techniques of quantum theory.
Dirac comes up with a relativistic quantum mechanical wave equation for the electron. Felix Bloch (1905-) suggests a theory of metals based on electrons layered periodic positive potentials which can sustain small displacements which lead to resistance via scattering of electrons by the lattice vibrations. John Clarke Slater (1900-1976) is the first to study the quantum mechanical treatment of the molecular formation of rare gases (helium). Linus Pauling (1901-) applies the Heitler-London treatment to chemical bonds. |
|
| 1929 |
Edmund Clifton Stoner (1899-1968), using (special) relativistic formulas for electron energies,
suggests that beyond a certain density in stars the outward degenerate gas pressure would no longer sustain
itself against the inward gravitational attraction (though he did not speculate about what would then happen).
Slater formulates a multi-electron wave function which can generally satisfy the Pauli exclusion principle. |
 John von Neumann |
| 1930 | Discovery of the lambda point of helium at which it becomes a superfluid (so-named in 1941) at 2.2°K. | |
| 1931 |
George David Birkhoff
(1884-1944) proves the general ergodic theoreom.
Pauling publishes his work on chemical bonds, proving the stability of such bonds. |
|
| 1932 | Aleksandr Yakovlevich Khinchin (1894-1959), in work through 1934, founds the modern study of stationary random processes. | |
| 1933 | Walther Meissner (1882-1974) and R Ochsenfeld report that metals cooled below their superconducting temperatures in a magnetic field completely expel all lines of magnetic induction, becoming a perfect diamagnet. | |
| 1934 |
William Lawrence Bragg (1890-1971)
and Williams formulates an Ising model for paramagnetic to ferromagnetic transitions.
Cornelius Jacobus Gorter (1907-1980) and Hendrik Bruygt Gerhard Casimir (1909-) form an analysis of the expulsion of magnetic fields in superconducting metals in a magnetic field. |
|
| 1935 |
William Francis Giauque achieves a temperature of only 0.1°K for helium using
a magnetic trap to slow the motion of the molecules.
Lev Davidovich Landau (1908-1968) publishes his phenomenological mean-field treatment for phase transitions. Subrahmanyan Chandrasekhar (1910-1995) derives the maximum mass formula for a degenerate Fermi gas. Fritz Wolfgang London (1900-1954) and brother Heinz London work on a superconductivity theory of macroscopic objects using classical electrodynamical theory and some additional assumptions. Hans Bethe (1906-) improves on Bragg-Williams theory by adding short-range atomic interactions. Edward Armand Guggenhaim (1901-) develops a theory of liquid solutions using nearest-neighbor rules, into what is now callod the "quasi-chemical" (QC) method. |
 Lev Landau |
| 1936 | Joseph Edward Mayer (1904-) (see links) and Sally F Harrison (1913-), along with Maria Goeppert-Mayer (1906-1972), initiate the modern theory of gas condensation, in work through 1938, by use of "cluster integrals" representing the interactions of many molecules to find the virial coefficients of intermolecular forces. | |
| 1937 |
Peter Leonidovich Kapitza (1894-?)
determines that helium II has a viscosity of about 1500 times smaller than helium I
and terms the phenomena "superfluidity." At almost the same time,
John Frank Allen (1908-) and A D Miscner
discover the same effect independently (publishing 19 days later).
John Edward Leonard-Jones (1894-1954) and A F Devonshire formulate (through '39) the "6-12 potential" for intermolecular forces. |
|
| 1938 |
Claude Elwood Shannon
(1916-) publishes A Symbolic Analysis of Relay and Switching Circuits, instigating the study of information
theory and giving a systematic way of mathematically treating noise.
London's theoretical work on liquid helium and Bose-Einstein condensation. |
 Claude Shannon |
| 1939 | W Conyer Herring calculates bulk properties of materials from quantum principles, specifically explaining how beryllium acts as a metal. | |
| 1940 | Fowler and Guggenheim extend the QC method, applying it to models which take into account longer-range interactions. | |
| 1942 | Lars Onsager (1903-1976) (also see links) gives his solution to the two-dimensional Lenz-Ising model, showing that a phase transition will occur. "[I]t is the first exact solution of a nontrivial problem in statistical mechanics, in which interparticle forces are taken into account without approximation" (SG Brush). | |
| 1944 | Evgenni Mikhailovich Lifshitz (1915-1985) shows that "second-sound" waves in superfluids can be detected as temperature deviations. The effect is experimentally confirmed shortly there after by V Peshkov. | |
| 1946 |
Nikolai Nikolaevich Bogolyubov (1909-) writes his Problems of Dynamical Theory in Statistical Physics.
He works on a generalization of the Boltzmann equation, using the time-reversal invariant Liouville equation,
further clarifying the internal structure of statistical mechanics.
Khinchin refines Boltzmann's theorem to read that, as a function of the size of an ensembles, the time average of a system becomes arbitrary close to the canonical average. Richard A Ogg, Jr suggests that pairs of electrons behave as bosons, and that superconductivity may be thought of as a Bose-Einstein condensate. (The idea is ignored until about 1954.) |
|
| 1948 | Shannon's major publication on information theory and symbolic logic, A Mathematical Theory of Communication. | |
| 1950 | Herbert Frölich (1905-) suggests that phonon interactions between electrons may be the basis of an explanation of superconductivity, giving one of the first uses of quantum field theory to statistical mechanics. | |
| 1953 | Richard Phillips Feynman (1918-1988) begins his work on the theory of superconducting helium using his path-integral approach, further clarifying how previous theoretical attempts have worked and/or failed. | |
| 1955 |
Erwin Wilhelm Mueller's (1911-1977) field ion microscope is the first instrument to allow imaging
of individual atoms.
W Noll proves that by taking the appropriate phase averages, any molecular system modelled by statistical mechanics can be shown to satisfy exactly the equivalent field equations for a continuous material, thus theoretically showing the equivalence of the two approaches. |
|
| 1956 | Leon Cooper (1930-), John Bardeen (1908-) and John Robert Schrieffer (1931-) form a many-electron theory of superconduction which gives good agreement with experiment and produces the Meissner effect. | |
| 1957 |
Khinchin's book,
Mathematical Foundations of Information Theory.
Berni Julian Alder (1925-) and Thomas Everett Wainwright (1927-) computationally discover the hard-sphere phase transition. |
|
| 1961 | George Allen Baker, Jr (1932-) found a method of determining the singularities at the critical point via series expansions of Lenz-Ising models. | |
| 1965 | Benjamin Widom's (1927-) work on surface tension theory using a modified van der Waals theory. | |
| 1968 | Alder and Wainwright discover vortex diffusion in liquids. | |
| 1971 | Kenneth Wilson (1936-), extending earlier work by Leo Kadanoff (in 1966), applies the technique of the renormalization group to study of scaling laws for phase transition theory. | |
| 1972 | Michel Ellis Fisher (1931-) and Widom show that the Lenz-Ising model generalized to arbitrary dimensions display a continuous transition between classical and non-classical laws, where correlation lengths tend toward infinity at critical points. | |
| 1980 | Heinrich Rohrer and Gerd Binnig develop the scanning tunnelling microscope, allowing for imaging of atoms embedded on surfaces. |
| Sources: |
Brush, Stephen G, Statistical Physics and the Atomic Theory of Matter From Boyle and Newton to Landau and Onsager (out of print) Bunch, Bryan & Hellemans, Alexander, The Timetables of Science Burr, Alex C, "Notes on the History of the Concept of Thermal Conductivity", Isis (20) Eisberg, R and Resnick, R, Quantum Physics, 2nd ed, 1985 Flamm, Dieter, "History and outlook of statistical physics," physics/9803005, 4 March, 1998 Flamm, Dieter, "Ludwig Boltzmann - A Pioneer of Modern Physics," physics/9710007, 7 October, 1997 Kuhn, Thomas S, Black-Body Theory and the Quantum Discontinuity, 1894-1912 Mendoza, E, "A Sketch for a History of Early thermodynamics," Physics Today, February 1961, p 32 Mendoza, E, "A Sketch for a History of the Kinetic Theory of Gases," Physics Today, March 1961 Mendelssohn, K, The Quest for Absolute Zero (out of print) Moore, Walter, Schrödinger: Life and Thought Purrington, Robert D, Physics in the Nineteenth Century Truesdell, C, Essays in the History of Mechanics (out of print) And the great MacTutor History of Mathematics Archive |
| Links: |
The Pneumatics of Hero of Alexandria Paul Charlesworth's History of Science pages Chris Hillman's Entropy in the Physical Sciences Biographies of chemists and some physicists available at the History of Chemistry page About Temperature by Project Skymath Fahrenheit's Paper of 1724 The Origin of the Celsius Temperature Scale Wave Mechanics: Louis de Broglie The Lars Onsager Archive Register of Joseph Mayer's Papers |